CARATTERISTICHE DELLE CURVE DI INDIFFERENZA

CARATTERISTICHE DELLE CURVE DI INDIFFERENZA

Dopo aver introdotto il concetto di curve di indifferenza, ora cercheremo di comprendere quali caratteristiche hanno tali curve.

La curva di indifferenza:

• ha un andamento decrescente;
• è una linea curva;
• è convessa verso l'origine degli assi;

Ognuna di queste caratteristiche corrisponde ad un preciso aspetto economico.

ANDAMENTO DECRESCENTE

L'andamento decrescente della curva di indifferenza è spiegabile in base al principio della non sazietà secondo il quale, tra due panieri, il consumatore sceglie sempre quello che contiene almeno una quantità maggiore di un bene a parità della quantità contenuta dell'altro bene.

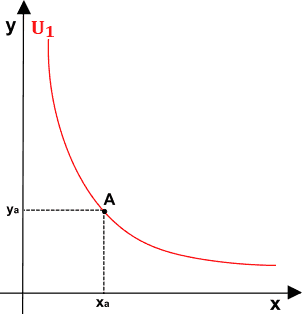
Disegniamo sugli assi cartesiani la curva di indifferenza U₁ e riportiamo su di essa il punto A a cui corrisponde:

• una quantità x_a del bene x;
• una quantità y_a del bene y.

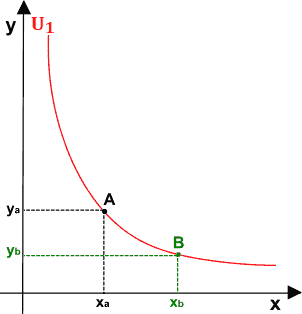
Ora consideriamo un punto B la cui ascissa sia x_b tale che:

x_b > x_a

Affinché il punto B si trovi sulla curva di indifferenza U₁ è necessario che la sua ordinata y_b sia inferiore rispetto a y_a perché altrimenti, l'utilità che il consumatore trarrebbe dal paniere B sarebbe maggiore rispetto a quella che trae dal paniere A e i due punti (A e B) non si troverebbero entrambi sulla curva U₁.

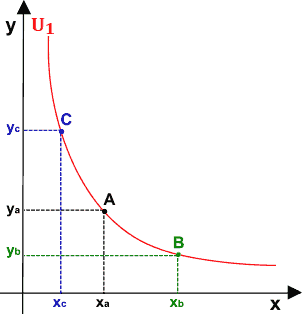
Ora consideriamo un punto C la cui ascissa sia x_c tale che:

x_c < x_a

Affinché il punto C si trovi sulla curva di indifferenza U₁ è necessario che la sua ordinata y_c sia maggiore rispetto a y_a perché altrimenti, l'utilità che il consumatore trarrebbe dal paniere C sarebbe minore rispetto a quella che trae dal paniere A e i due punti (A e C) non si troverebbero entrambi sulla curva di indifferenza U₁.

Ecco spiegato il perché della pendenza negativa della curva di indifferenza.

Se la curva di indifferenza avesse pendenza positiva significherebbe che, per il consumatore, due panieri sarebbero indifferenti anche se uno di essi contenesse una maggiore quantità sia del bene x che del bene y rispetto all'altro paniere.

CONVESSITA' VERSO L'ORIGINE DEGLI ASSI

La curva di indifferenza presenta una convessità verso l'origine degli assi. Cerchiamo di capire il perché di questo andamento.

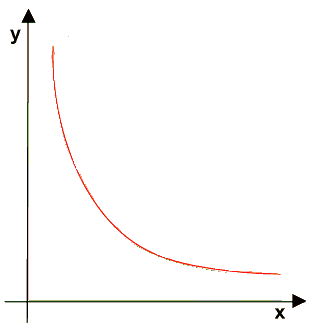
Mano a mano che ci spostiamo da sinistra verso destra diminusice la disponibilità del bene y. Di conseguenza, poiché l'utilità marginale dei beni è decrescente, l'importanza del bene y aumenta per il consumatore e, quantità sempre minori del bene y saranno sufficienti a rimpiazzare quantità costanti del bene x.

Allo stesso modo, spostandoci sulla curva di indifferenza sempre da sinistra verso destra la disponibilità del bene x aumenta, di conseguenza la sua importanza diminuisce per il consumatore e, saranno necessarie quantità sempre maggiori del bene x per rimpiazzare quantità costanti del bene y.

Quindi, il fatto che la curva di indifferenza sia convessa verso l'origine degli assi è dovuta all'utilità marginale di un bene che è sempre decrescente.

Il fatto che la curva di indifferenza è convessa verso l'origine degli assi significa anche che, normalmente, il consumatore preferisce disporre di panieri bilanciati, cioè formati da quantità più o meno simili di entrambi i beni, piuttosto che panieri formati da grossi quantitativi di un solo tipo di bene e pochissime quantità dell'altro.

Chiaramente, essendo la curva di indifferenza convessa, essa è anche una linea curva.

CASI PARTICOLARI

Le caratteristiche che abbiamo qui visto relative alla curva di indifferenza sono valide nella gran parte dei casi. Tuttavia esistono dei casi particolari nei quali essa si presenta con una forma diversa e, di conseguenza, la sua pendenza non è negativa e non ci troviamo di fronte ad una curva.

Ripetiamo, però, che si tratta di casi particolari di cui parleremo quando ci soffermeremo sulle diverse forme che può avere la curva di indifferenza.