CURVA DEL PRODOTTO MEDIO E CURVA DEL PRODOTTO MARGINALE

CURVA DEL PRODOTTO MEDIO DEL LAVORO

Abbiamo visto che il prodotto medio del lavoro non è altro che il rapporto tra la quantità ottenuta dal processo produttivo e la quantità di lavoro impiegata per ottenerla.

Dal punto di vista matematico, data la funzione del prodotto totale, il prodotto medio del lavoro in un dato punto è dato dalla pendenza della retta passante per l'origine degli assi e per tale punto.

Poiché noi sappiamo che la pendenza di una retta dipende dal suo coefficiente angolare possiamo dire che il prodotto medio del lavoro in un dato punto è uguale al coefficiente angolare della retta passante, per questo punto, e per l'origine degli assi.

ESEMPIO

Cerchiamo di capire quanto abbiamo detto attraverso un esempio.

Riprendiamo i dati visti in precedenza e disegniamo la funzione del prodotto totale e la funzione del prodotto medio.

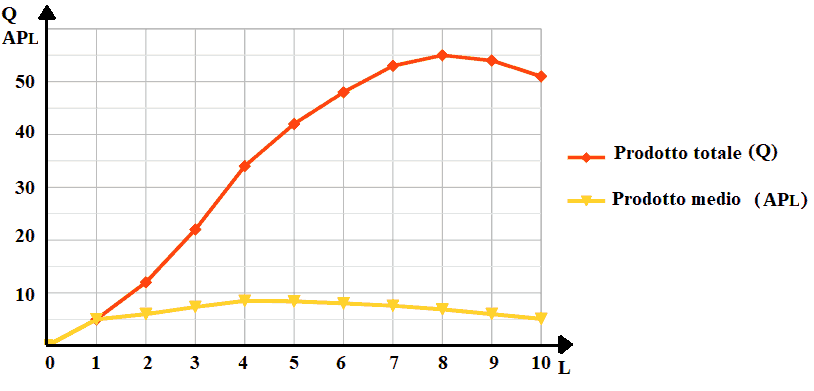
Scegliamo un punto sulla funzione del prodotto totale, ad esempio il punto A di cooordinate

A(2; 12)

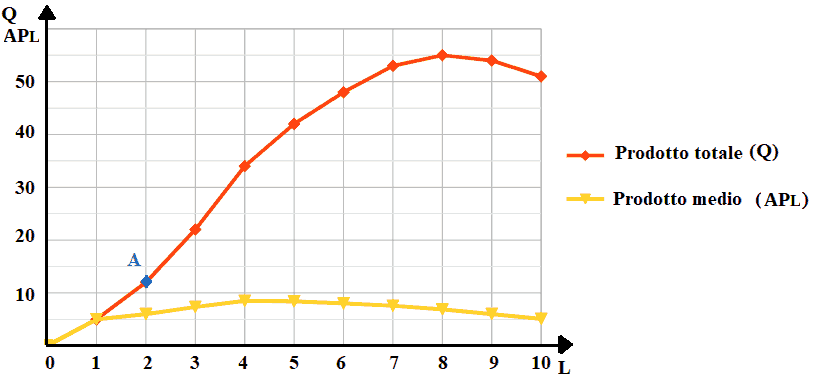
Ora disegniamo la retta passante per l'origine degli assi e per il punto A.

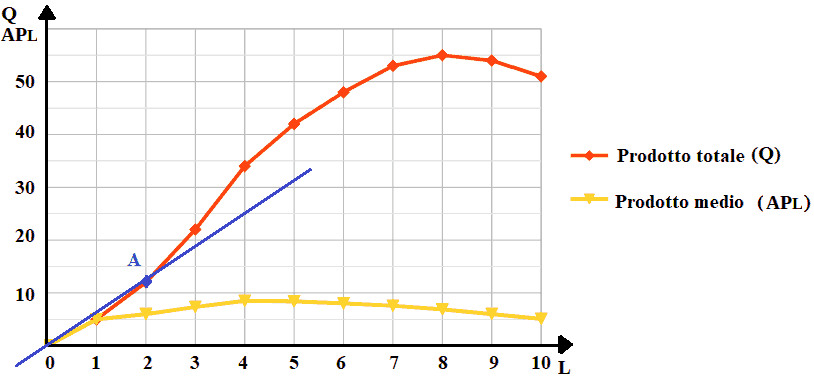
Noi sappiamo che l'equazione di una retta passante per l'origine degli assi è del tipo:

y = m·x

dove m è il coefficiente angolare e varia col variare della pendenza della retta.

Ora vogliamo dimostrare che il prodotto medio calcolato nel punto A è pari a 6.

Per farlo scriviamo l' equazione della retta passante per due punti ed esattamente per l'origine degli assi e per il punto A.

La formula da applicare è la seguente:

(y - y₀)/(y₁ - y₀) = x - x₀)/(x₁ - x₀)

Sostituiamo le coordinate dell'orgine degli assi e del punto A ed otteniamo:

(y - 0)/(12 - 0) = (x - 0)/(2-0)

Eseguiamo i calcoli ed abbiamo:

y/12 = x/2

Moltiplichiamo per 12 entrambi i membri:

y = 6·x

Il coefficiente angolare è pari a 6 esattamente come il prodotto medio nel punto A.

Chiaramente possiamo ripetere il procedimento per ogni punto della funzione del prodotto totale giungendo sempre alla stessa conclusione.

CURVA DEL PRODOTTO MARGINALE DEL LAVORO

Come si è detto in precedenza il prodotto marginale del lavoro è dato dall'incremento della quantità prodotta in seguito all'incremento di una unità del fattore lavoro.

Dal punto di vista matematico, data la funzione del prodotto totale, il prodotto marginale del lavoro in un dato punto è dato dalla pendenza della retta tangente alla curva del prodotto totale nel punto stesso.

Dato che abbiamo detto che la pendenza di una retta dipende dal suo coefficiente angolare possiamo affermare che il prodotto marginale del lavoro in un dato punto è uguale al coefficiente angolare della retta tangente alla curva del prodotto totale in quel punto.

ESEMPIO

Riprendiamo ancora una volta i dati visti in precedenza e disegniamo la funzione del prodotto totale e la funzione del prodotto marginale.

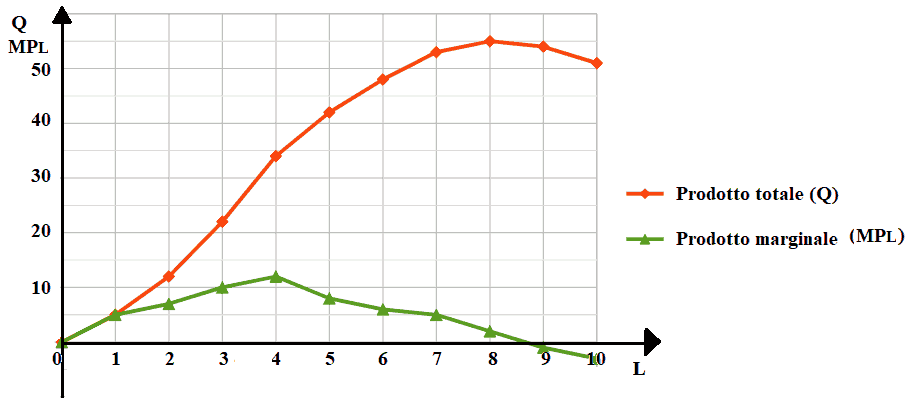
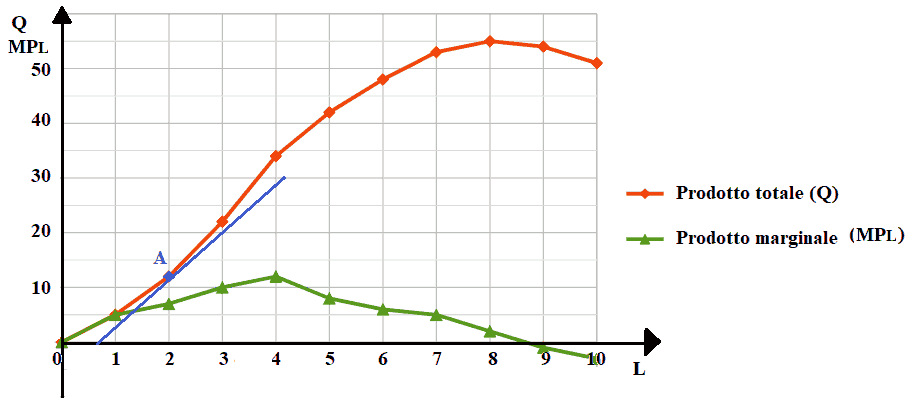
Scegliamo un punto sulla funzione del prodotto totale: anche in questo caso scegliamo il punto A di cooordinate

A(2; 12)

e disegniamo la retta tangente alla curva del prodotto totale nel punto A.

Data una funzione

y = f(x)

noi sappiamo che il coefficiente angolare della retta tangente al suo grafico in un dato punto non è altro che la derivata della funzione stessa in quel punto.

A sua volta, la derivata di una funzione è il limite, per x che tende a zero, del rapporto incrementale (Δy/Δx). Quest'ultimo rappresenta la produttività marginale del lavoro, ovvero ΔQ/ΔL.